Modulated longitudinal gates on encoded spin-qubits via curvature couplings to a superconducting cavity
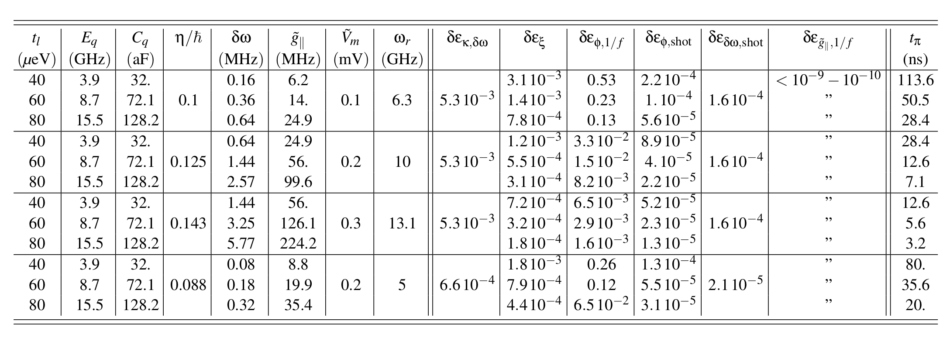
We propose entangling operations based on the energy curvature couplings of encoded spin qubits to a superconducting cavity, exploring the non-linear qubit response to a gate voltage variation. For a two-qubit (n-qubit) entangling gate we explore acquired geometric phases via a time-modulated longitudinal σz-coupling, offering gate times of 10s of ns even when the qubits and the cavity are far detuned. No dipole moment is necessary: the qubit transverse σx-coupling to the resonator is zero at the full sweet spot of the encoded spin qubit of interest (a triple quantum dot three-electron exchange-only qubit or a double quantum dot singlet-triplet qubit). This approach allows always-on, exchange-only qubits, for example, to stay on their “sweet spots” during gate operations, minimizing the charge noise and eliminating an always-on static longitudinal qubit-qubit coupling. We calculate the main gate errors due to the (1) diffusion (Johnson) noise and (2) damping of the resonator, the (3) 1/f-charge noise qubit gate dephasing and 1/f-noise on the longitudinal coupling, (4) qubit dephasing and ac-Stark frequency shifts via photon fluctuations in the resonator, and (5) spin-dependent resonator frequency shifts (via a “dispersive-like” static curvature coupling), most of them associated with the non-zero qubit energy curvature (quantum capacitance). Using spin-echo-like error suppression at optimal regimes, gate infidelities of 10−2−10−3 can be achieved with experimentally existing parameters. The proposed schemes seem suitable for remote spin-to-spin entanglement of two spin-qubits or a cluster of spin-qubits: an important resource of quantum computing.